Let’s discuss the question: how to parametrize a triangle. We summarize all relevant answers in section Q&A of website Achievetampabay.org in category: Blog Finance. See more related questions in the comments below.
Can you parameterize a triangle?
mathmari said: So, the parametrization of the triangle has to satisfy the equation of the plane. Yep.
What is the parametric equation of a triangle?
Parametric Equation for a Triangle
Let P(t) be that point along the AB edge of the triangle. The second parameter, say s, is the parameter of a line from vertex C to P(t). That is, the endpoint of the second line is a moving target. The point Q(s,t) is a point in the triangle, on a line between C and P(t).
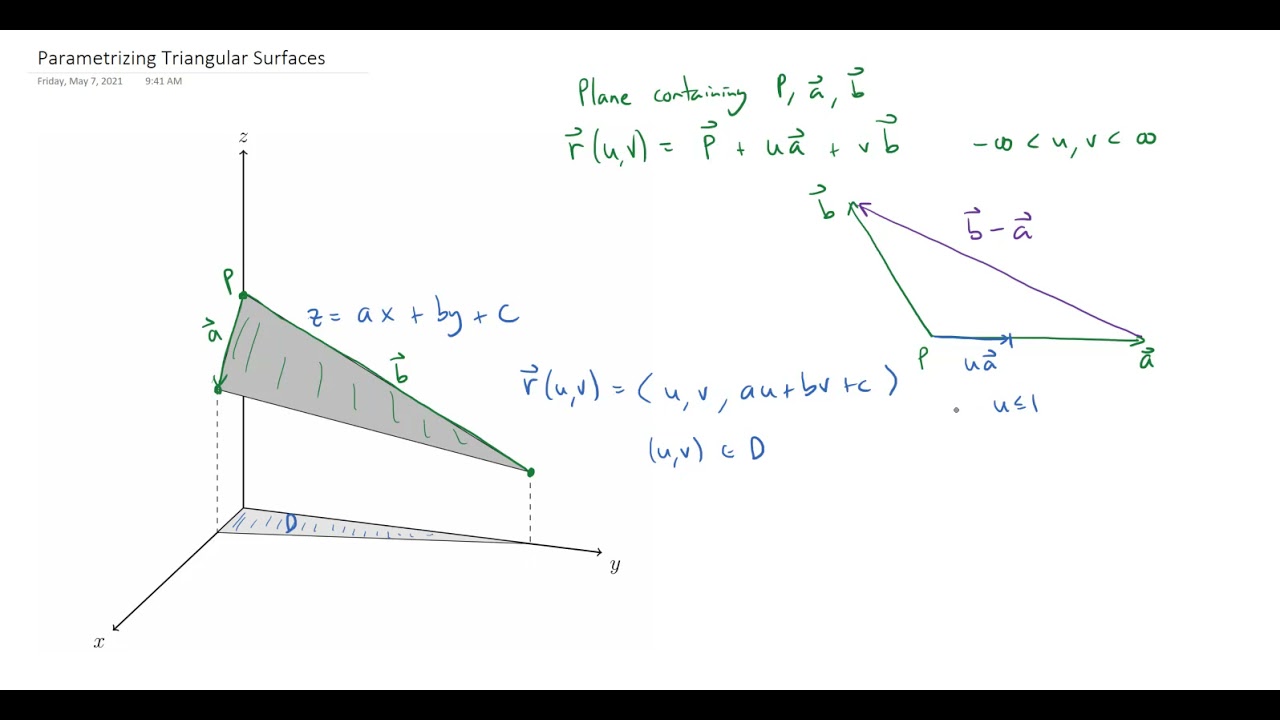
Parametrizing Triangular Surfaces
Images related to the topicParametrizing Triangular Surfaces

How do you find the parametric equation of a plane?
To find a parametrization, we need to find two vectors parallel to the plane and a point on the plane. Finding a point on the plane is easy. We can choose any value for x and y and calculate z from the equation for the plane. Let x=0 and y=0, then equation (1) means that z=18−x+2y3=18−0+2(0)3=6.
What is the benefit of using parametric equations?
One of the advantages of parametric equations is that they can be used to graph curves that are not functions, like the unit circle. Another advantage of parametric equations is that the parameter can be used to represent something useful and therefore provide us with additional information about the graph.
What is smooth parametrization?
Definition: smoothness. Let ⇀r(t)=f(t)ˆi+g(t)ˆj+h(t)ˆk be the parameterization of a curve that is differentiable on an open interval I. Then ⇀r(t) is smooth on the open interval I, if. ⇀r′(t)≠⇀0, for any value of t in the interval I.
What is a piecewise smooth curve?
1The precise definition of a piecewise smooth curve is that you want the derivative ˙c(t) = (˙x(t), ˙y(t)) to exist. and be continuous for all except maybe finitely many t ∈ [a, b], and the side limits limt→t± 0. ˙x(t) to exist for all t0 ∈ [a, b].
How do you solve a surface integral?
- Chop up the surface S into many small pieces.
- Multiply the area of each tiny piece by the value of the function f on one of the points in that piece.
- Add up those values.
How do you find the parametric equation of a function?
- Find a set of parametric equations for the equation y=x2+5 .
- Assign any one of the variable equal to t . (say x = t ).
- Then, the given equation can be rewritten as y=t2+5 .
- Therefore, a set of parametric equations is x = t and y=t2+5 .
Ex 1A: Determine a Piecewise Smooth Parameterization for a Curve (Triangle)
Images related to the topicEx 1A: Determine a Piecewise Smooth Parameterization for a Curve (Triangle)

What does parameterized mean in math?
In mathematics, and more specifically in geometry, parametrization (or parameterization; also parameterisation, parametrisation) is the process of finding parametric equations of a curve, a surface, or, more generally, a manifold or a variety, defined by an implicit equation.
What is an implicit equation for a plane?
An implicit function is one given by F: f(x,y,z)=k, where k is a constant. Unlike the other two examples, the tangent plane to an implicitly defined function is much more difficult to find. As with graphs and parametric plots, we must use another device as a tool for finding the plane.
How do you find the sides of a triangle?
- if leg a is the missing side, then transform the equation to the form when a is on one side, and take a square root: a = √(c² – b²)
- if leg b is unknown, then. b = √(c² – a²)
- for hypotenuse c missing, the formula is. c = √(a² + b²)
How is a2 b2 c2?
The Pythagorean Theorem describes the relationship among the three sides of a right triangle. In any right triangle, the sum of the areas of the squares formed on the legs of the triangle equals the area of the square formed on the hypotenuse: a2 + b2 = c2.
What is formula for area of triangle?
The area of a triangle is defined as the total region that is enclosed by the three sides of any particular triangle. Basically, it is equal to half of the base times height, i.e. A = 1/2 × b × h.
Is parametric form infinite?
As you can see that the solution was actually a parametric solution meaning that there are infinite possible solutions.
Parametrization Around a Triangle
Images related to the topicParametrization Around a Triangle

How do you convert to parametric form?
Converting from rectangular to parametric can be very simple: given , the parametric equations , produce the same graph. As an example, given y = x 2 – x – 6 , the parametric equations x = t , y = t 2 – t – 6 produce the same parabola.
What does T stand for in parametric equations?
By Meltem Ucal • Edit History. Table of Contents. parametric equation, a type of equation that employs an independent variable called a parameter (often denoted by t) and in which dependent variables are defined as continuous functions of the parameter and are not dependent on another existing variable.
Related searches
- parameterize triangle in 3d
- parameterize an equation
- parametrize a rectangle
- how to parameterize a surface
- how to find angles of a triangle in a triangle
- parameterization z x 2 y 2
- what is the parameter of a triangle
- how to parametrize a line
- parameterization of a curve
- triangle in a triangle symbol
- parametrize a disk
- parametric equation of triangle
- how to solve a triangle in a triangle
- parameterization z x 2 + y 2
- how to parametrize a triangle in r3
Information related to the topic how to parametrize a triangle
Here are the search results of the thread how to parametrize a triangle from Bing. You can read more if you want.
You have just come across an article on the topic how to parametrize a triangle. If you found this article useful, please share it. Thank you very much.